| sex | status | income | verbal | gamble |
|---|---|---|---|---|
| female | 51 | 2.00 | 8 | 0.0 |
| female | 28 | 2.50 | 8 | 0.0 |
| female | 37 | 2.00 | 6 | 0.0 |
| female | 28 | 7.00 | 4 | 7.3 |
| female | 65 | 2.00 | 8 | 19.6 |
| female | 61 | 3.47 | 6 | 0.1 |
Introduction
This analysis aims to understand the factors that influence teenage gambling expenditure. We will explore the relationships between gambling expenditure and gender and income. It is our hypothesis that both gender and income should affect gambling expenditure among teenagers.
Data
The analysis is based on data from (Ide-Smith and Lea 1988) published in the Journal of Gambling Behavior. It comes from a survey that was conducted to study teenage gambling in Britain.
The key variables are:
- sex
- status : Socioeconomic status score based on parents’ occupation
- income : Weekly income in pounds
- verbal : verbal score in words out of 12 correctly defined
- gamble : expenditure on gambling in pounds per year
A cursory look at the data suggests that females likely spend less on gambling compared to males. Additionally that most females do not spend more than approx. 20£ per year on gambling.
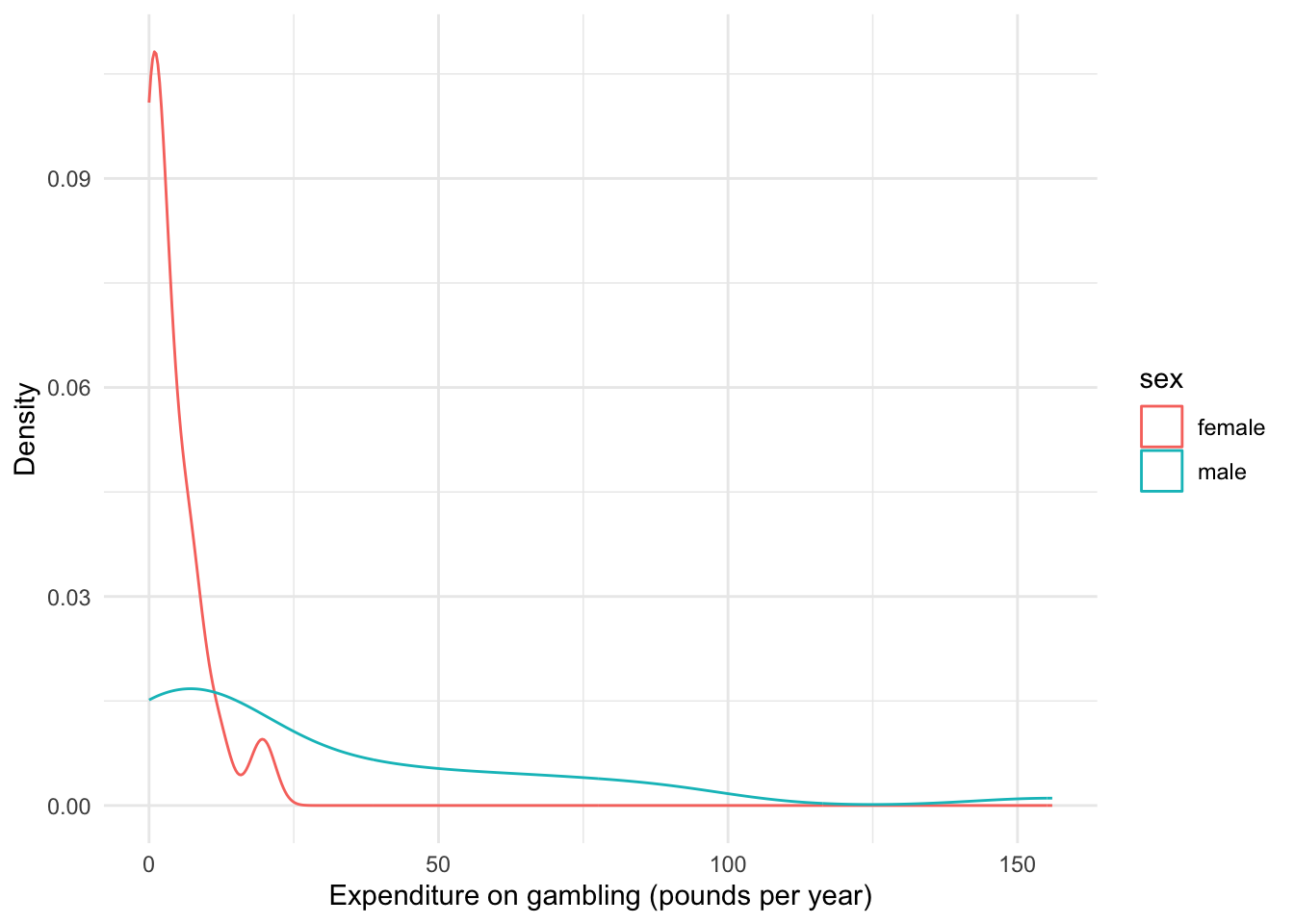
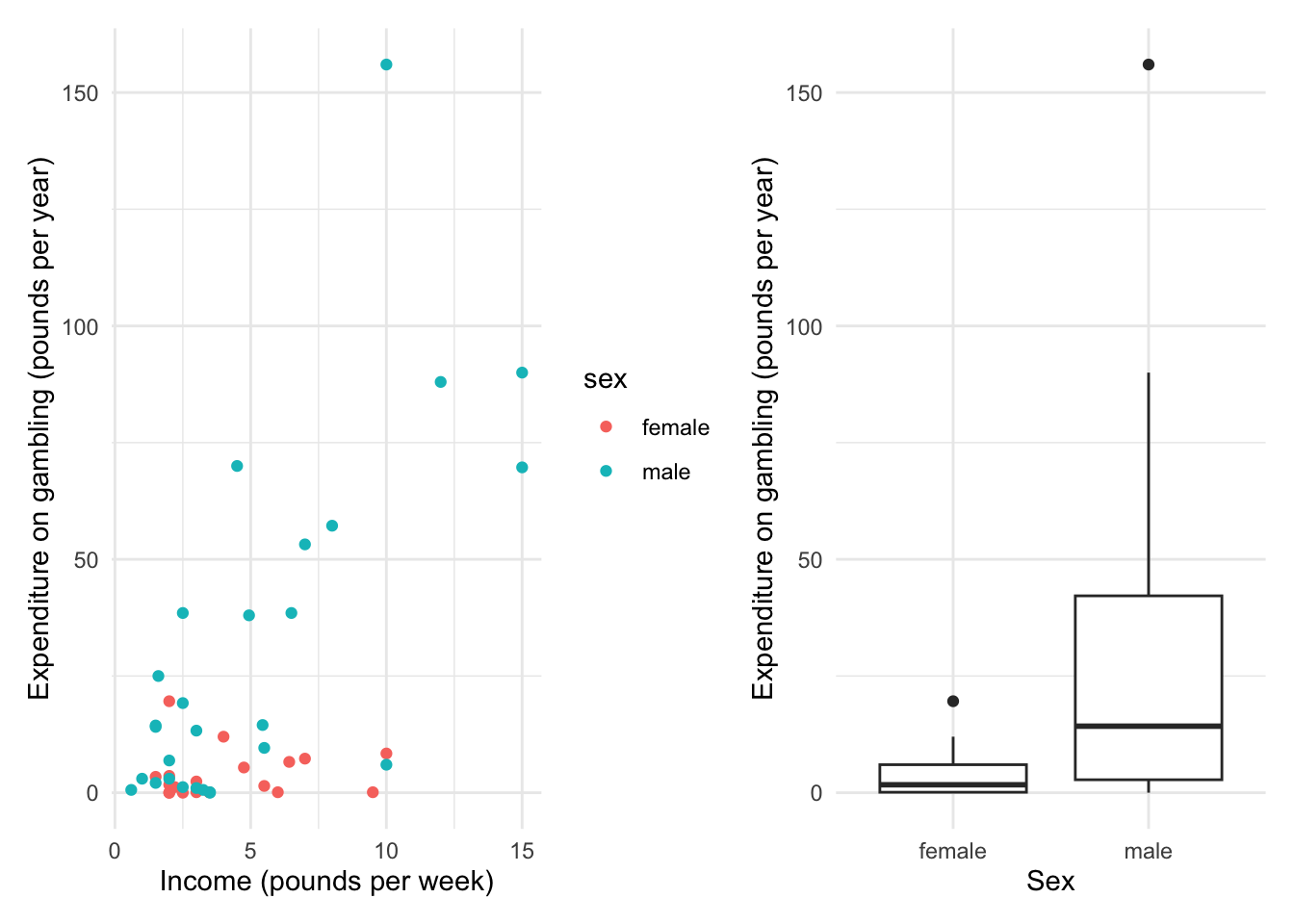
There also seems positive association between income and amount spent on gambling (at least for males). This is not very surprising as one would expect that individuals with higher income would be able to spend more on gambling.
From what this plot indicates, it may be worth evaluating if there is a differential effect of income based on gender.
Analysis
Our variable of interest gamble is strictly positive and continuous with a long tail. We consider taking log of gamble value. This alters the interpretation of model mechanics but it remains sensible, e.g. males spend x% more than females or 1£ increase in income leads to y% increase in expenditure in gambling.
Side note: This is different from using GLM with Gaussian family and log link. Because in original scale, variance is non constant and multiplicative effects are expected on original scale of response (as opposed to expected value of response).
To be able to take logarithms of cases where 0£ are spent on gambling, 1£ is added to gambling spent for all cases. This value is chosen to ensure 0 for cases where 0£ are spent and values close to 0 for small spends, additionally this does not introduce un necessary -ve outlier values resulting in better fit.
Individual 24 seems to have spent 156£ on gambling and likely seems an outlier. This seems to be outside the usual range of expenditure and will not inform the study in a general sense. Hence, we remove this point from the analysis.
Effect of Gender
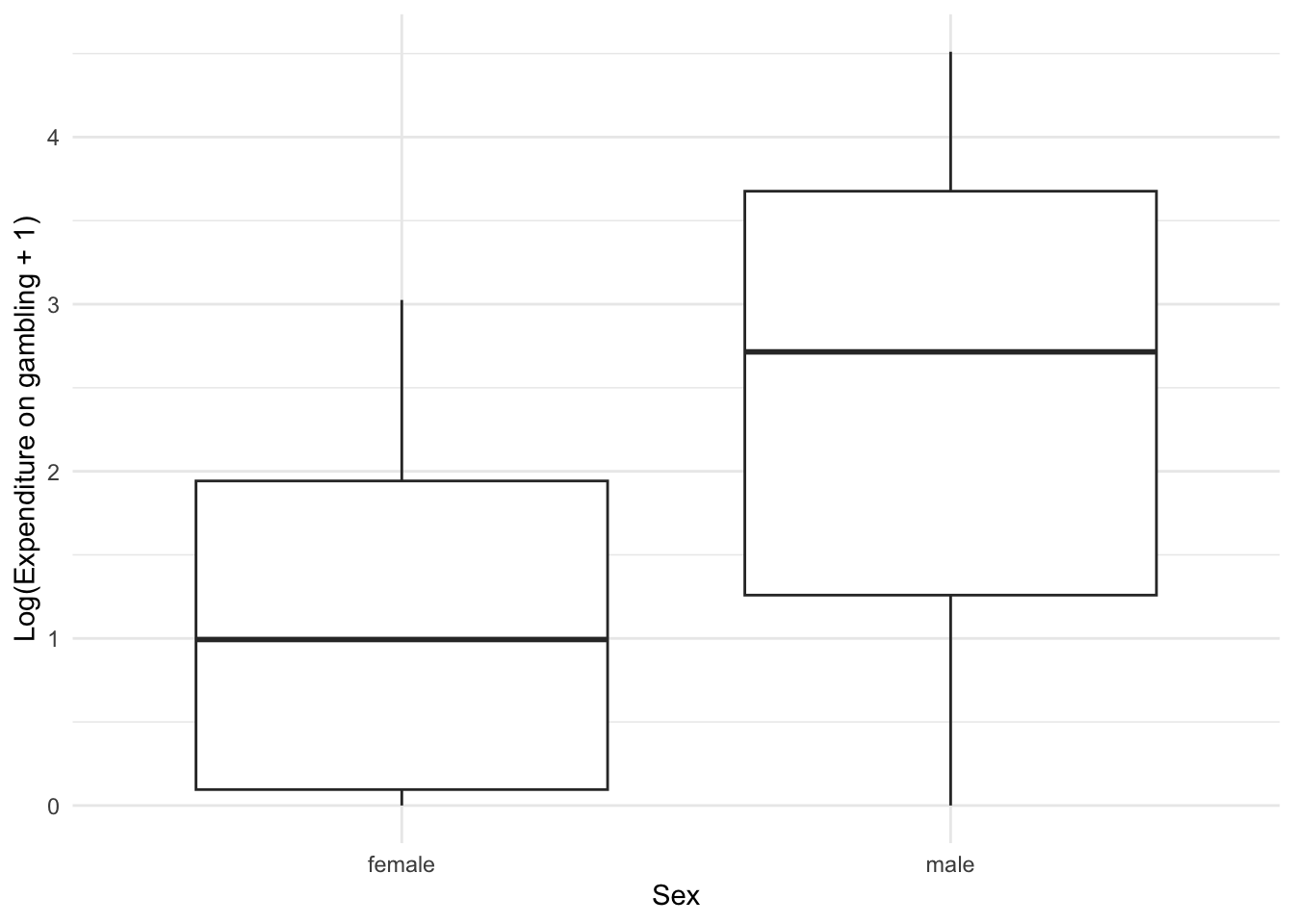
It seems plausible that males are spending more on gambling compared to females. This is also indicated by the boxplot below. We will evaluate this hypothesis using a simple linear model with log(gamble + 1) as response and sex as explanatory variable.
Analysis of Variance Table
Response: log_gamble
Df Sum Sq Mean Sq F value Pr(>F)
sex 1 20.365 20.365 12.261 0.001074 **
Residuals 44 73.085 1.661
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Gender seems to have statistically significant association with gambling expenditure.
Anova procedure is equivalent to a t-test with constant variance assumption (Faraway 2025), which seems fair from the Boxplot above. They test for the same effect and result in identical p-values.
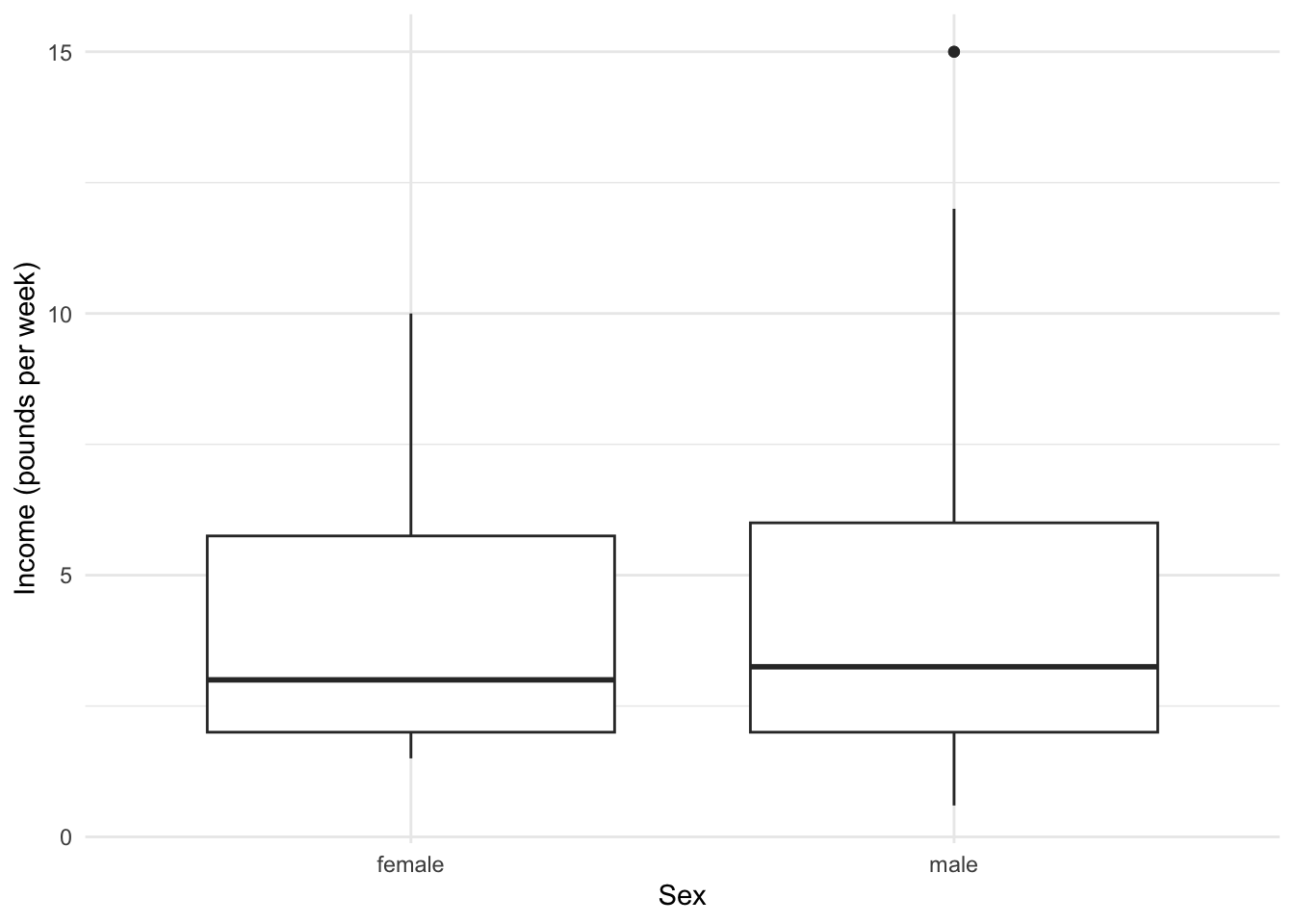
Before moving to analysing joint effect of Income and Gender, it is imperative to check if the effect of gender is not due to confounding by income. It could well be the case that individuals with higher income spend more on gambling. But then if high income itself is associated with gender, then the above effect of gender may be spurious. We will explore this next.
Analysis of Variance Table
Response: income
Df Sum Sq Mean Sq F value Pr(>F)
sex 1 4.58 4.5754 0.3685 0.5469
Residuals 44 546.25 12.4149 The above plot and the test indicates that income is not significantly associated with gender and hence does not mask its effect on gambling expenditure.
For the analysis that follows, we shall print the summary of gender only model to show the Estimate value and Std. Error of gender.
summary(gender_model)
Call:
lm(formula = log_gamble ~ sex, data = teengamb)
Residuals:
Min 1Q Median 3Q Max
-2.4630 -1.0616 0.1547 1.0979 2.0478
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.1117 0.2957 3.760 0.000498 ***
sexmale 1.3513 0.3859 3.502 0.001074 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.289 on 44 degrees of freedom
Multiple R-squared: 0.2179, Adjusted R-squared: 0.2002
F-statistic: 12.26 on 1 and 44 DF, p-value: 0.001074Effect of Gender and Income
With income variable included alongside sex, the effect of sex remains significant (although is reduced from 1.35 to 1.24 with lower Std. Error).
Income itself is significantly associated with gambling expenditure.
The intercept is non-significant indicating that for reference class (female), gambling expenditure is likely 0£ if they have close to 0 income and it makes intuitive sense (although for adults and addicts this may not necessarily be true).
This model does not include an interaction between sex and income for simplificty, yet fits the data well. Model diagnostics also appear acceptable.
Call:
lm(formula = log_gamble ~ sex + income, data = teengamb)
Residuals:
Min 1Q Median 3Q Max
-2.2327 -0.7944 0.1318 0.8419 2.2973
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.37092 0.33009 1.124 0.267373
sexmale 1.23699 0.34216 3.615 0.000782 ***
income 0.17852 0.04869 3.667 0.000671 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.138 on 43 degrees of freedom
Multiple R-squared: 0.4042, Adjusted R-squared: 0.3765
F-statistic: 14.59 on 2 and 43 DF, p-value: 1.46e-05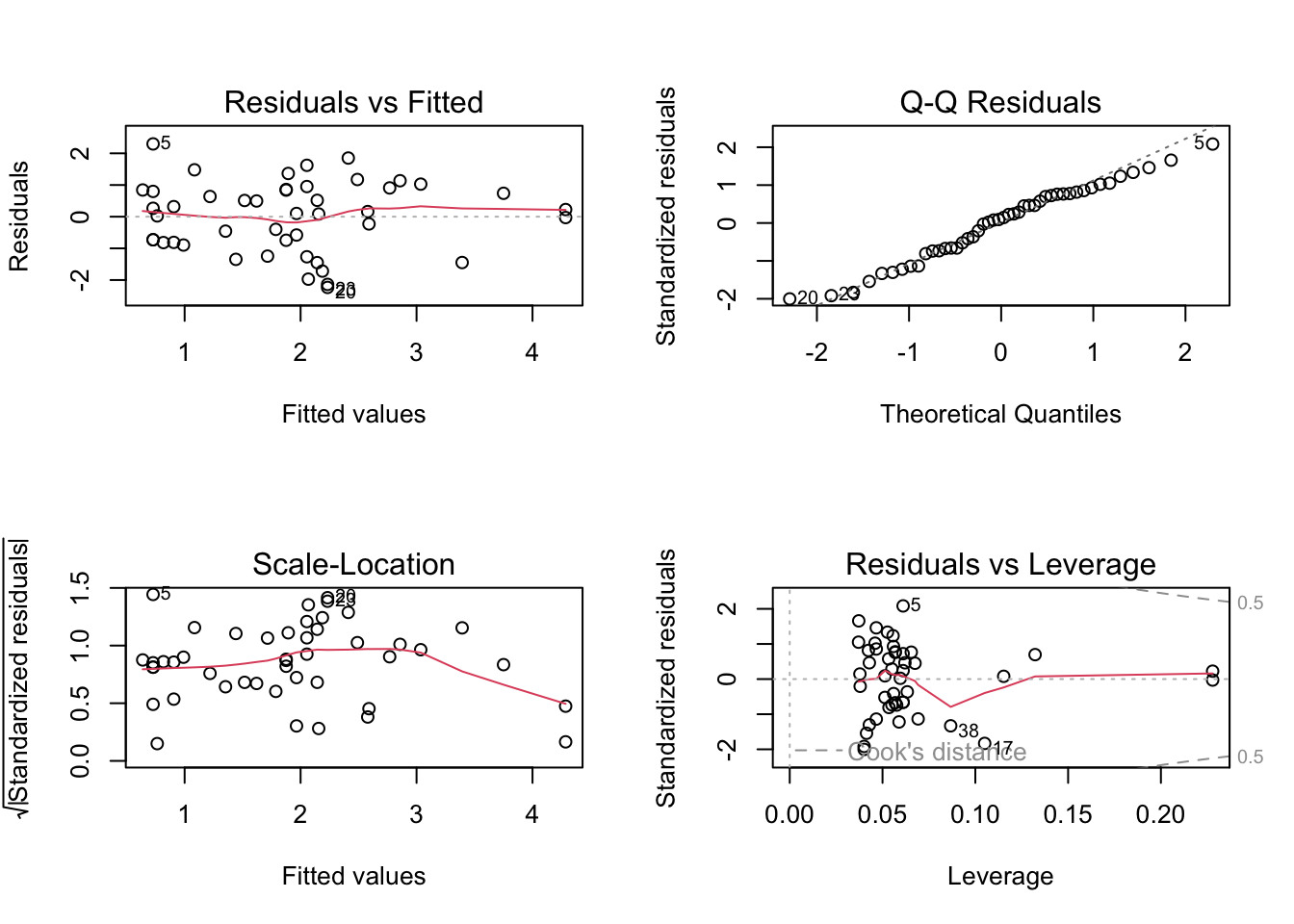
Additionally, the residuals do not indicate any obvious pattern with respect to gender.
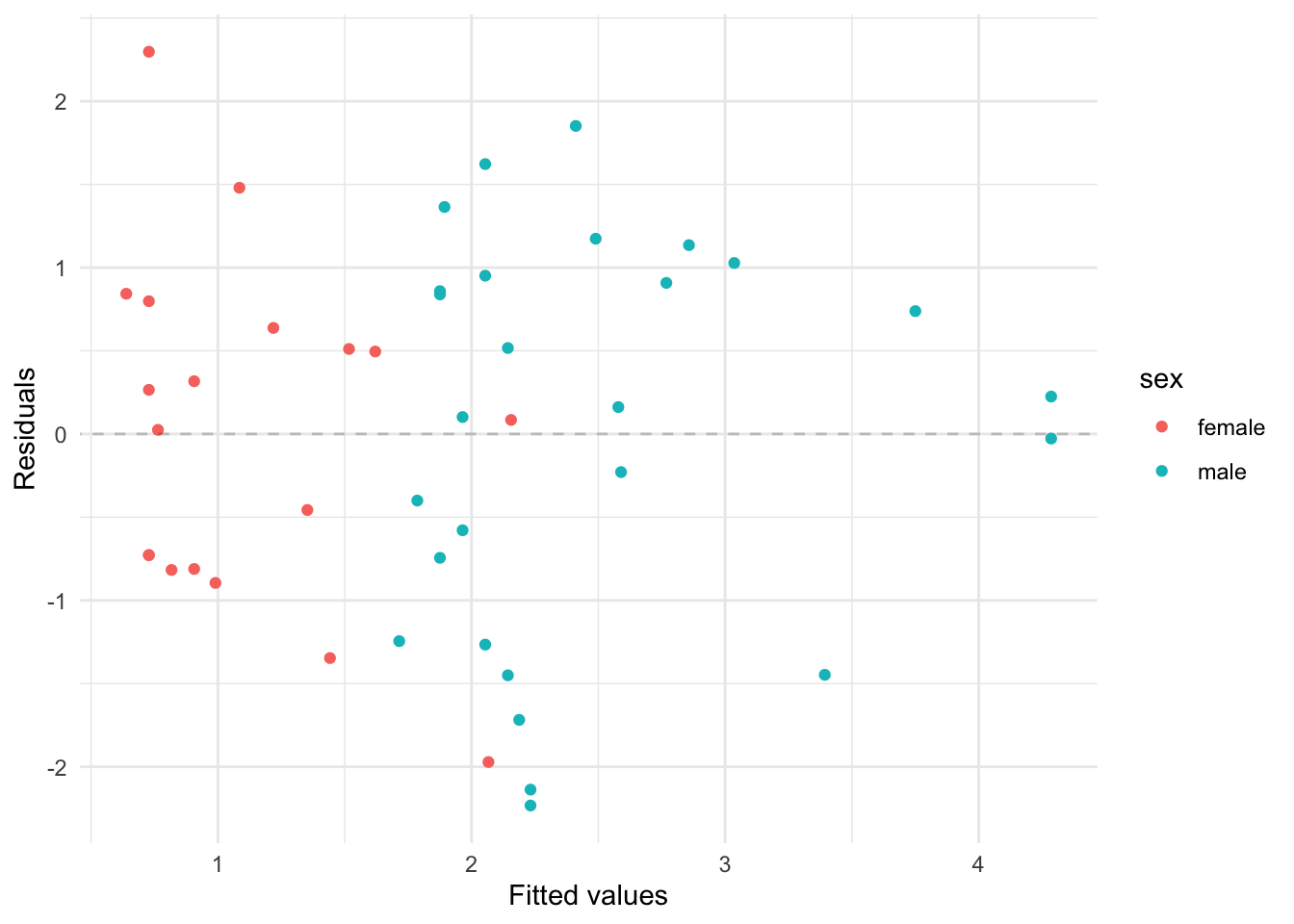
From an earlier observation, it was suspected that there could be differential effect of income on expenditure based on gender. The current model (lines) seems to indicate that there might be some difference between how males and females respond to changes in income.
We shall try to fit an interaction between sex and income to evaluate if this is indeed the case.
It appears as though the interaction does not improve the model fit compared to no interaction model.
Analysis of Variance Table
Model 1: log_gamble ~ sex * income
Model 2: log_gamble ~ sex + income
Res.Df RSS Df Sum of Sq F Pr(>F)
1 42 53.517
2 43 55.676 -1 -2.1582 1.6938 0.2002Additionally, interaction term is not significant and so it is best to remove it and keep the model simple.
Call:
lm(formula = log_gamble ~ sex * income, data = teengamb)
Residuals:
Min 1Q Median 3Q Max
-2.1894 -0.9791 0.0763 0.8456 2.0447
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.85855 0.49761 1.725 0.0918 .
sexmale 0.58832 0.60303 0.976 0.3348
income 0.06101 0.10240 0.596 0.5545
sexmale:income 0.15114 0.11613 1.301 0.2002
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.129 on 42 degrees of freedom
Multiple R-squared: 0.4273, Adjusted R-squared: 0.3864
F-statistic: 10.45 on 3 and 42 DF, p-value: 2.921e-05Conclusion
The analysis indicates that both gender and income are significantly associated with gambling expenditure among teenagers.
Males tend to spend 3x more than females on gambling (even at comparable income levels). This effect may be inflated to some degree since boys tended to exaggerate their gambling spend and girls tended to under-report them (Ide-Smith and Lea 1988).
A 1£ increase in weekly income is associated with a 19% increase in annual gambling expenditure.
The interaction between gender and income was not significant, indicating that the effect of income on gambling expenditure is similar for both genders.
References
Faraway, Julian J. 2025. Linear Model with r, Third Edition. CRC Press.
Ide-Smith, Susan G., and Stephen E. G. Lea. 1988. “Gambling in Young Adolescents.”